Cryptomancy | Writeup challenge Barbhack2025 (Crypto) | Centre d'expertises en cybersécurité

Introduction

La BARBHACK est un événement de cybersécurité organisé à Toulon au mois d’août. On y retrouve des conférences, une session de rump, un barbecue ainsi qu’un CTF en clôture de journée.

Acceis a constitué une équipe de cinq joueurs pour participer au CTF et grâce au renfort de deux membres de l’entreprise Bsecure, nous avons décroché la 2ᵉ place du classement final.

Parmi les épreuves, un challenge de cryptographie fondé sur les courbes elliptiques a particulièrement retenu notre attention. Nous avons choisi d’en proposer un writeup détaillé.

Découverte du challenge

La plateforme de CTF nous fournit deux choses :

Le code source du challenge en python (cryptomancy.py)
Un accès TCP au challenge: cryptomancy.ctf.barbhack.fr:1337

L’application est codée en python et voici son code source :

from secret import FLAG
from ecc_utils import get_ecc_setup, generate_keypair, modinv, ECDSASignature, generate_random_nonce

from Crypto.Util.asn1 import DerSequence
from hashlib import sha256
import base64
import json

private_key, public_key = generate_keypair(get_ecc_setup())

challenge_banner = r"""
.--------------------------------------------------------------------.
|   ____                  _                                          |
|  / ___|_ __ _   _ _ __ | |_ ___  _ __ ___   __ _ _ __   ___ _   _  |
| | |   | '__| | | | '_ \| __/ _ \| '_ ` _ \ / _` | '_ \ / __| | | | |
| | |___| |  | |_| | |_) | || (_) | | | | | | (_| | | | | (__| |_| | |
|  \____|_|   \__, | .__/ \__\___/|_| |_| |_|\__,_|_| |_|\___|\__, | |
|             |___/|_|                                        |___/  |
'--------------------------------------------------------------------'
"""
message_menu = """
Welcome to the forgery! You can forge multiple tokens here, but only our true sheriff can access the secret.
Please choose what to do:
1 - Create a user
2 - Retrieve the secret
3 - Quit the program
"""

def sign(priv, msg):
    G = priv.ecc_setup.G
    n = priv.ecc_setup.n

    msg_hash = int.from_bytes(sha256(msg).digest(), "big")

    while True:
        # I made sure k is not over n-1
        k = generate_random_nonce()
        V = k * G
        r = V.x % n
        if r == 0:
            print(f"r={r}")
            continue
        s = (modinv(k, n) * (msg_hash + priv.d * r)) % n
        if s == 0:
            print(f"s={s}")
            continue
        break

    signature = ECDSASignature(r, s)
    return signature

def verify_signature(pub, msg, signature):
    n = pub.ecc_setup.n
    G = pub.ecc_setup.G
    r = signature.r
    s = signature.s

    def num_ok(nb):
        return 1 < nb < (n - 1)

    if not num_ok(r):
        raise ValueError(f"Invalid signature value: r={r}")
    if not num_ok(s):
        raise ValueError(f"Invalid signature value: s={s}")

    msg_hash = int.from_bytes(sha256(msg).digest(), "big")
    h = modinv(s, n)

    h1 = (msg_hash * h) % n
    h2 = (r * h) % n

    P = h1 * G + h2 * pub.W
    r1 = P.x % n
    return r1 == r

def create_user(username):
    """
    format:
    user: string - name of the user
    role: string - "user" or "admin" which gives permissions
    """
    headers = {"alg": "ES256", "typ": "JWT"}
    payload = {"username": username, "role": "user"}

    result = [
        base64.urlsafe_b64encode(json.dumps(headers).encode()).replace(b"=", b""),
        base64.urlsafe_b64encode(json.dumps(payload).encode()).replace(b"=", b"")
    ]
    to_sign = b".".join(result)

    r, s = sign(private_key, to_sign)
    signature = DerSequence((r, s)).encode()

    result.append(base64.urlsafe_b64encode(signature).replace(b"=", b""))
    result = ".".join([p.decode("utf-8") for p in result])

    return result

def decode_token(token):
    try:
        headerb64, payloadb64, signatureb64 = [t + "==" for t in token.split(".")] # add max padding as unnecessary padding will be removed
    except:
        return None

    header = json.loads(base64.urlsafe_b64decode(headerb64))
    payload = json.loads(base64.urlsafe_b64decode(payloadb64))

    if header["typ"] == "JWT" and header["alg"] == "ES256":
        try:
            signed_message = token[:token.rfind(".")]
            der_signature = base64.urlsafe_b64decode(signatureb64)
            signature = ECDSASignature(DerSequence().decode(der_signature)[0], DerSequence().decode(der_signature)[1])
            if verify_signature(public_key, signed_message.encode(), signature):
                return payload
            else:
                return None
        except:
            return None
    else:
        return None

def get_secret(token):
    informations = decode_token(token)
    if informations is not None:
        if informations["role"] == "sheriff":
            print(f"Hello {informations['username']}. You are our true sheriff, here is your secret: {FLAG}")
        else:
            print(f"Hello {informations['username']}. You are not our sheriff, get out!")
    else:
        print("Invalid token")

def main():
    print(f"Server public key: \n{public_key}")
    print(challenge_banner)

    while True:
        print(message_menu)
        user_input = input("What are you doing ? > ")
        match user_input:
            case "1":
                username = input("Choose your username > ")
                created_user_token = create_user(username)
                print(f"Here is your token: {created_user_token}")
            case "2":
                token = input("Enter your token > ")
                get_secret(token)
            case "3":
                print("bye bye")
                exit(0)

if __name__ == "__main__":
    main()

Une première remarque importante : les sources ne sont pas complètes. La seconde ligne du code importe des éléments absents, car le fichier ecc_utils.py n’est pas fourni !

from ecc_utils import get_ecc_setup, generate_keypair, modinv, ECDSASignature, generate_random_nonce

Nous devons donc nous concentrer sur le fonctionnement global de l’application. Comme souvent dans ce type de challenge, l’auteur met à disposition un oracle de signature ECDSA permettant de signer des messages (ici : des tokens). Le but est de produire une signature valide pour un message spécifique, ce qui permet de récupérer le flag.

La fonction get_secret gère la vérification du rôle contenu dans le token:

def get_secret(token):
    informations = decode_token(token)
    if informations is not None:
        if informations["role"] == "sheriff":
            print(f"Hello {informations['username']}. You are our true sheriff, here is your secret: {FLAG}")
        else:
            print(f"Hello {informations['username']}. You are not our sheriff, get out!")
    else:
        print("Invalid token")

Concrètement :

l’utilisateur choisit un username,
ce nom est passé à la fonction create_user,
cette fonction construit puis signe un token.

def create_user(username):
    """
    format:
    user: string - name of the user
    role: string - "user" or "admin" which gives permissions
    """
    headers = {"alg": "ES256", "typ": "JWT"}
    payload = {"username": username, "role": "user"}

    result = [
        base64.urlsafe_b64encode(json.dumps(headers).encode()).replace(b"=", b""),
        base64.urlsafe_b64encode(json.dumps(payload).encode()).replace(b"=", b"")
    ]
    to_sign = b".".join(result)

    r, s = sign(private_key, to_sign)
    signature = DerSequence((r, s)).encode()

    result.append(base64.urlsafe_b64encode(signature).replace(b"=", b""))
    result = ".".join([p.decode("utf-8") for p in result])

    return result

On observe que le champ role est toujours fixé à user.
L’objectif est donc de parvenir à modifier ce champ et à obtenir un token valide où role=sheriff.

Analyse de l’implémentation ECDSA

L’ECDSA (Elliptic Curve Digital Signature Algorithm) est une variante de l’algorithme DSA reposant sur l’arithmétique des courbes elliptiques.
Il permet de signer un message de façon à garantir son authenticité et son intégrité, sans révéler la clé privée.
La sécurité repose sur la difficulté du problème du logarithme discret sur les courbes elliptiques (ECDLP).

Rappels sur les courbes elliptiques

Ref: LostCertificate | Writeup challenge leHack2024 (Crypto)

Les courbes elliptiques sont des objets mathématiques avec des applications importantes en cryptographie, en théorie des nombres et dans de nombreux autres domaines de la mathématique.

Une courbe elliptique est l’ensemble des solutions (x,y) dans un corps fini Fp vérifiant une équation du type:

 $y^2=x^3+a*x+b$

Augmenté d’un point à l’infini noté O, qui sert d’élément neutre pour la loi de groupe sur la courbe

Pour que l’ensemble des solutions forme une courbe de Weierstrass au sens strict, il est nécessaire que le discriminant de l’équation, donné par :

 $\Delta=-16*(4*a^3)+27*b^2$

soit non nul.
Cette condition assure que la courbe n’a pas de points singuliers, c’est-à-dire de cusps ou de croisements.

Dans notre cas, le challenge utilise la courbe secp256r1, les paramètres sont les suivantes:

 $p = 115792089210356248762697446949407573530086143415290314195533631308867097853951 \newline a = 115792089210356248762697446949407573530086143415290314195533631308867097853948 \newline b = 41058363725152142129326129780047268409114441015993725554835256314039467401291 \newline$

Points à l’infini

En plus des points sur le plan, les courbes elliptiques incluent également un point à l’infini, noté

$O$

qui sert d’élément neutre pour l’addition de points sur la courbe.

Définition des paramètres (E, G, n)

E : la courbe elliptique
G: le point générateur (ou "base point"), choisi sur la courbe, qui engendre un sous-groupe cyclique d’ordre n
n : l’ordre de G. C’est le plus petit entier tel que n*G = O. n est premier ce qui garantit que Z/nZ est un corps. La primalité de n une condition nécessaire pour que les inverses de chaque point existent.

Addition des points

L’addition de deux points sur une courbe elliptique est définie géométriquement. Pour additionner deux points P et Q on procède de la manière suivante :

Tracer une ligne droite passant par P et Q
Cette ligne coupera la courbe en un troisième point R’
Le point R, qui est l’addition P+Q est le reflet de R’ par rapport à l’axe des abscisses

Cas particuliers

Addition d’un point à lui-même (doublage)
Pour doubler un point P = (x, y), on utilise la formule suivante pour trouver 2*P :

 $s = \frac{3x^2 + a}{2y} \newline x_{2P} = s^2 - 2x \newline y_{2P} = s(x - x_{2P}) - y$

Addition avec le point à l’infini:
Pour tout point P:

 $P + \mathcal{O} = \mathcal{O} + P = P$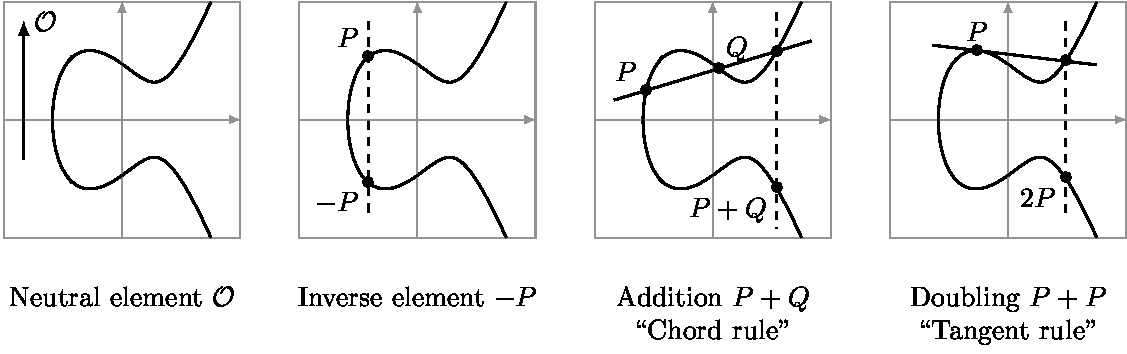

Multiplication des points

La multiplication d’un point P par un entier n est simplement l’addition de
P à lui-même n fois.
Cette opération peut être effectuée efficacement en utilisant l’algorithme de doublement et addition, aussi connu sous le nom de "méthode des doubles et des ajouts".

La structure constitue un groupe abélien : les points sur la courbe elliptique, munis de l’opération géométrique d’addition, forment un ensemble

fermé
associatif
doté d’un élément neutre (le point à l’infini) et d’inverses pour chaque point
l’addition est commutative

Cette propriété (groupe abélien) est essentielle pour les opérations cryptographiques. En effet la multiplication scalaire k*G est aisée à calculer, mais à l’inverse; trouver k connaissant G et k*G est bien plus diffcile.

Ce problème est appelé ECDLP (Problème du logarithme discret appliqué au courbes elliptiques) et est le fondement du protocole ECDSA.

Le Problème du Logarithme Discret sur les Courbes Elliptiques (ECC)

Le problème du logarithme discret elliptique (ECDLP) est l’analogue du problème du logarithme discret dans les courbes elliptiques, similaire à celui rencontré dans d’autres groupes algébriques comme les groupes multiplicatifs des corps finis.

Définition du problème

Sur une courbe elliptique, le problème du logarithme discret peut être formulé comme suit :

étant donné deux points P et Q sur une courbe elliptique, trouver un entier k tel que :

 $Q = k*P$

où k est le "logarithme" de Q à la base P.
En d’autres termes, k est le facteur de multiplication scalaire qui, lorsqu’il est appliqué à P, produit Q.

Difficulté du problème

La sécurité de nombreux systèmes de cryptographie basés sur les courbes elliptiques, repose sur la difficulté de résoudre ce problème du logarithme discret.

Comparé à son équivalent dans les groupes multiplicatifs des corps finis, le problème du logarithme discret sur les courbes elliptiques est généralement plus difficile à résoudre pour des tailles de clé équivalentes.

Cela permet d’utiliser des clés plus courtes tout en maintenant un niveau de sécurité comparable, ce qui se traduit par des gains en termes d’efficacité et de performance.

Fonctionnement de ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA (Elliptic Curve Digital Signature Algorithm) est une variante de l’algorithme de signature numérique DSA qui utilise les propriétés des courbes elliptiques pour améliorer la sécurité et l’efficacité. Voici comment il fonctionne, étape par étape.

1. Prérequis

Pour utiliser ECDSA, il est nécessaire de disposer :

D’une courbe elliptique E sur un corps fini Fp
D’un point de base G sur E, dont l’ordre (nombre de multiple de G avant de retomber sur le point à l’infini) est un grand nombre premier n.

2. Génération des clés

Clé privée : Le signataire choisit un nombre aléatoire d compris entre 1 et n−1. Ce nombre d sert de clé privée.
Clé publique : La clé publique Qest calculée en multipliant le point de base G par la clé privée *d:

 $Q = d*G$

3. Signature d’un message

Pour signer un message m, le signataire procède comme suit :

Hachage du message: Calculer le hachage H(m) du message à signer m, ou H est une fonction de hachage cryptographique tel que la famille des shaX. Ce hash est ensuite réduit modulo n pour obtenir z.
Génération d’un nombre aléatoire : Choisir un nombre aléatoire k entre 1 et n-1
Calcul de coordonnées du point : Calculer le point k*G=(x1, y1) et appliquer le modulo n à x1 afin d’obtenir r. (Si r=0, choisir un autre k et recommencer.)
Calcul de la signature : On calcule

 $s = k^{-1}*(z + rd) \pmod{n}$

(Si s=0, on recommence avec une autre valeur de *k*)

Pour résumer, on a :

 $k = random(1, n-1) \newline z = H(m) \pmod{n} \newline r = (k * G).x \pmod{n} \newline s = k^{-1}*(z + r*d) \pmod{n}$

La signature est le couple (r, s)

Le code qui se charge de cette partie est le suivant:

def sign(priv, msg):
    G = priv.ecc_setup.G
    n = priv.ecc_setup.n

    msg_hash = int.from_bytes(sha256(msg).digest(), "big")

    while True:
        # I made sure k is not over n-1
        k = generate_random_nonce()
        V = k * G
        r = V.x % n
        if r == 0:
            print(f"r={r}")
            continue
        s = (modinv(k, n) * (msg_hash + priv.d * r)) % n
        if s == 0:
            print(f"s={s}")
            continue
        break

    signature = ECDSASignature(r, s)
    return signature

A première vue, le code semble fidèle au fonctionnement standart de ECDSA. On peut donc passer à la partie Vérification de la signature.

4. Vérification de la Signature

Pour vérifier la signature (r, s) d’un message m avec la clé publique Q, on effectue les étapes suivantes :

Vérifier les paramètres : S’assurer que r et s sont compris entre 1 et n-1
Hachage du message :
Soit H la fonction de hashage, ici hashlib.sha256, on a :
```
 $z = H(m) \pmod{n}$ 
```
Calcule de l'inverse de s:
```
 $w = s^{-1} \pmod{n}$ 
```

Calculer u1 et u2:

 $u_1 = z*w \pmod{n} \newline u_2 = r*w \pmod{n}$

Calculer le point X:
```
 $X = u_1*G + u_2*Q$ 
```
(Si X est le point à l'infini, alors la signature est invalide.)
Calculer v : La coordonnée x de X modulo n donne v.
Si `v = r`, la signature est valide. Sinon, elle est invalide.

La fonction `verify_signature` est la suivante:

def verify_signature(pub, msg, signature):
    n = pub.ecc_setup.n
    G = pub.ecc_setup.G
    r = signature.r
    s = signature.s

    def num_ok(nb):
        return 1 < nb < (n - 1)

    if not num_ok(r):
        raise ValueError(f"Invalid signature value: r={r}")
    if not num_ok(s):
        raise ValueError(f"Invalid signature value: s={s}")

    msg_hash = int.from_bytes(sha256(msg).digest(), "big")
    h = modinv(s, n)

    h1 = (msg_hash * h) % n
    h2 = (r * h) % n

    P = h1 * G + h2 * pub.W
    r1 = P.x % n
    return r1 == r

Aprés avoir passé plusieurs minutes à lire le code du challenge, il semblerai que le protocol ECDSA soit correctement implémenté … du moins, avec la partie de code qui est fourni.

Application à notre challenge.

Afin d'intéragir avec le challenge, nous avons utilisé la librairie `pwntools` en python et codé un wrapper afin de communiquer avec les différentes options. Avec la librairie `ecdsa` nous avons ainsi pu créer tout les objets nécessaires à ECDSA et ainsi commencer à travailler avec nos objets mathématiques.

Voici le début du wrapper:

from pwn import *
import base64
import json
from hashlib import sha256
from Crypto.Util.asn1 import DerSequence
from Crypto.Util.number import inverse
from ecdsa.ellipticcurve import CurveFp, Point, INFINITY
from ecdsa.ecdsa import Public_key

# secp256r1
p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
a = 115792089210356248762697446949407573530086143415290314195533631308867097853948
b = 41058363725152142129326129780047268409114441015993725554835256314039467401291
E = CurveFp(p, a, b)

Gx = 48439561293906451759052585252797914202762949526041747995844080717082404635286
Gy = 36134250956749795798585127919587881956611106672985015071877198253568414405109
n  = 115792089210356248762697446949407573529996955224135760342422259061068512044369
G = Point(E, Gx, Gy, n)

Wx = 3001868853520017179332280791962079322605515828679424799022137411657927415516
Wy = 100691011922509539575864881995020402308895975667049595800037405946637905658093
W = Point(E, Wx, Wy, n)

pub = Public_key(G, W)

assert E.contains_point(G.x(), G.y())
assert E.contains_point(W.x(), W.y())
assert (G * n) == INFINITY

IP = "cryptomancy.ctf.barbhack.fr"
PORT = 1337

context.log_level = 'critical'
io = remote(IP, PORT)

print("="*100)
print(f"p = {p}")
print(f"a = {a}")
print(f"b = {b}")
print()
print(f"n: {n}")
print(f"G: {Gx}:{Gy}")
print(f"W: {Wx}:{Wy}")
print("="*100)

def create_token(username: bytes):
    io.recvuntil(b'What are you doing ? > ')
    io.sendline(b'1')
    io.recvuntil(b'> ')
    io.sendline(username)
    data = io.recvline().split(b': ')[1].decode().strip()
    h = get_data(username.decode())
    return data, h

def submit_token(token: str):
    io.recvuntil(b'What are you doing ? > ')
    io.sendline(b'2')
    io.recvuntil(b'> ')
    io.sendline(token.encode())
    data = io.recvline().decode().strip()
    return data

io.recvuntil(b'Server public key: \n')
pub = io.recvline().decode().strip()

Les fonctions `create_token` et `submit_token` nous permettent respectivement de signer les messages avec un utilisateur que nous controllons et envoyer un token pour récuperer le flag.

Découverte de la vulnérabilté

L'ensemble du code fournis semble cohérent avec une implémentation fidèle de ECDSA. Cependant, un commentaire dans le code a retenu notre attention :

# I made sure k is not over n-1
k = generate_random_nonce()

La génération du nonce repose ici sur la fonction generate_random_nonce(). Cette fonction provient de ecc_utils.py, fichier auquel nous n'avons pas accès. Il nous est donc impossible d'étudier la façon dont k est généré, ni de vérifier qu'il est bien uniformément aléatoire dans l'intervalle [1, n−1] et jamais réutilisé.

Dès lors, une question se pose : pourquoi cette partie est-elle critique et potentiellement vulnérable ?

Pour rappel dans ECDSA,

 $r = (k * G).x \bmod n \newline s = k^{-1}*(z + rd) \bmod n$

Si le même k est utilisé pour deux messages (donc même r), il est possible de récupérer k, puis la clé privée d :

 $k = (z_1 - z_2)\,(s_1 - s_2)^{-1} \bmod n,\qquad d = (s_1 k - z_1)\, r^{-1} \bmod n$

Si k est statique, prévisible (exemples : générateur d'aléa non sûr, graine faible fondée sur le temps, etc.) ou parfois en dehors de [1, n−1] puis réduit modulo n, il est possible d'observer des collisions de r ou réduire drastiquement l'entropie effective de k, rendant l'attaque ainsi faisable.

Le commentaire " k is not over n-1" indique au mieux un contrôle de bornes, mais ne garantit pas l'unicité de k par signature, que k soit réellement aléatoire, ni l'application de la RFC 6979 qui utilise un générateur de nombres aléatoires déterministe (HMAC_DRBG ou HKDF) pour calculer k.

En partant de ces observations, nous avons cherché à identifier une réutilisation du nonce k, ce qui se traduit par l'apparition d'un même r dans deux signatures distinctes. Pour cela, nous avons généré dans un premier temps deux tokens signés et extrait les couples (r, s). En comparant les deux valeurs de r, nous avons constaté qu'elles étaient différentes, indiquant que k n'est pas strictement statique. Cela suggère néanmoins que la réutilisation du nonce pourrait se produire après plusieurs signatures. Sur cette base, nous avons généré plusieurs tokens supplémentaires et extrait leurs couples (r, s) jusqu'à observer une collision sur r.

Ainsi, à partir de deux signatures partageant le même r, nous avons pu calculer le nonce k, puis en déduire la clé privée d. Grâce à cette clé, nous avons signé un token arbitraire ayant un payload attribuant le rôle sheriff, que nous avons ensuite soumis pour valider le challenge.

def evil_user(private_key):
    headers = {"alg": "ES256", "typ": "JWT"}
    payload = {"username": "admin", "role": "sheriff"}
    result = [
        base64.urlsafe_b64encode(json.dumps(headers).encode()).replace(b"=", b""),
        base64.urlsafe_b64encode(json.dumps(payload).encode()).replace(b"=", b"")
    ]
    to_sign = b".".join(result)
    r, s = sign(private_key, to_sign)
    signature = DerSequence((r, s)).encode()
    result.append(base64.urlsafe_b64encode(signature).replace(b"=", b""))
    result = ".".join([p.decode("utf-8") for p in result])
    return result

seen = {}
i = 0
collision = None

while True:
    i += 1
    uname = f"user{i}".encode()
    tok, z1 = create_token(uname)
    _, __, sig_jwt = decodeur(tok)
    sig = DerSequence().decode(base64.urlsafe_b64decode(sig_jwt))
    r1, s1 = sig[0], sig[1]

    if r1 in seen:
        z2, r2, s2, tok2 = seen[r1]
        if (s1 - s2) % n == 0:
            continue
        collision = ((z2, s2, tok2), (z1, s1, tok))

        print(r1, s1, z1)
        print(r2, s2, z2)

        k=((z1 - z2) * inverse(s1 - s2, n)) % n
        r_inv = inverse(r1,n)
        private_key = ((s1*k - z1) * r_inv) % n
        sheriff = evil_user(private_key)
        flag = submit_token(sheriff)
        print(flag)

        break
    else:
        seen[r1] = (z1, r1, s1, tok)

    if i % 500 == 0:
        print(f"[.] Tokens générés: {i}")

Résultat

Voici le résultat final:

====================================================================================================
p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
a = 115792089210356248762697446949407573530086143415290314195533631308867097853948
b = 41058363725152142129326129780047268409114441015993725554835256314039467401291

n: 115792089210356248762697446949407573529996955224135760342422259061068512044369
G: 48439561293906451759052585252797914202762949526041747995844080717082404635286:36134250956749795798585127919587881956611106672985015071877198253568414405109
W: 3001868853520017179332280791962079322605515828679424799022137411657927415516:100691011922509539575864881995020402308895975667049595800037405946637905658093
====================================================================================================
40869495586588205422022465188607979887685504585867624747431504967932851687958 54815659014611583418253766532525985622448401964471507083820036820020873079112 87684154038605242987545440731271868368289105553478523537270116085190664937811
40869495586588205422022465188607979887685504585867624747431504967932851687958 15221458125872290068304969937060354268129467871845068797719458320635440326341 12008574295307831965777608033749850136942725992674460627922513257891984189564
Hello admin. You are our true sheriff, here is your secret: brb{w3_<3_0uR_5h3r1ff_3v3n_1F_h3_1s_4_b1T_Cr4zY}

Cryptomancy | Writeup challenge Barbhack2025 (Crypto)